You see the player advancing towards the goal, clearly trying to score. But the goalkeeper doesn’t stand his ground. He runs towards the player instead of staying on the post. Why would he do that? The reason is maths!
Football is often referred to as “O jogo bonito”, Portuguese for The beautiful game’ – a nickname popularised by the Brazilian great, Pele. And rightly so.
Just like any other beautiful movement, football requires rhythm, coordination, and balance. And at the same time, it also requires skill. However, just being a master at tackling, shooting or goalkeeping does not necessarily make you a great player.
Some of the best football players on the field today are also terrific mathematicians, who use maths in football. The instinctive understanding of the concepts of geometry, speed-distance-time, and calculus which they utilise isn’t determined by the ability to solve equations on a blackboard. And this application itself gives them the edge over other players. If you’ve watched the popular television show Ted Lasso, you will probably understand this claim by watching the coaches and players strategising how to tackle their opponents So, how is maths used in football? Let’s look at calculations used by players for some of the most common goals and defence strategies in this beautiful game:
United we stand! Tiki taka football strategy
A great example of real-time use of geometry to create space and beat defenders is the tiki taka-a popular method that became the talk of town when Spain claimed the Euro Cup and the World Cup in 2008 and 2010. This is a systematic approach to football founded upon team unity and a comprehensive understanding in the geometry of space on a football field.
How do players perform tiki taka?
The football players try to form triangles all around the pitch to maintain the ball possession, making it difficult for the opponent to obtain the ball and organise their game. Tiki taka has proven to be very successful as a football strategy.
Eyes on the prize. Goalkeeper’s one on one
One of the best examples where football and maths go hand in hand is distracting a striker. The goal is to create a larger obstruction to reduce the space available to score, hence lowering the probability of a goal
Often when a striker is in a one-on-one situation with the goalkeeper (like in our introduction), the latter charges towards the striker rapidly to close the space thereby reducing the angle and space available to strike the ball. This is another successful ideology of mathematical football.
How to hit a chip shot?
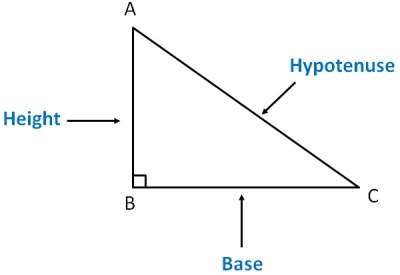
One of the most beautiful moves in football is chipping a charging goalkeeper. As the space reduces, the cool minded striker notices the increase in space to score. A 3-dimensional view allows the striker to kick over the charging goalkeepers head, and into the goalpost.
The chip shot, which is quite popular among both fans and players, doesn’t require power, rather a deft touch that follows a perfect parabola into the net.
Know thy enemy! Save thy penalties
Teams these days are aware of the past penalties taken by players. Most players follow a pattern in their penalty shots and this analysis of the previous shots puts the keeper in a much better situation to predict the next shot.
Goal posts: to go square or to go round?
The goalposts we see now are circular and have an elliptical cross-section. The goalposts before 1987 had the square cross-section. This invariably meant that most of the shots that hit the posts, came out instead of going in which brought unnecessary disappointment to the teams.
Does football strategy need data analysts and mathematicians?
While football maths was initially used for strategising the buying and selling of players, it is now integrated to what it can also do on the tactical analysis of the game.
Believe it or not, almost every football team today has a team of mathematicians or statisticians who help the coach define football strategies based on data. A huge amount of data is collected and analysed to understand opposing teams game-play, strengths and weaknesses of players, and to define tactics.
For example, if two players pass the ball 300 times to each other on average in a game, what kind of advantage can the opposition gain by reducing their total number of passes to 100?
Football tessellation
One very obvious example of mathematical football is the shape of the ball itself. The most familiar spherical polyhedron is the ball used in football, thought of as a spherical truncated icosahedron.
What does football tessellation mean?
The football is usually made of white hexagon shapes and black pentagon shapes – this is an example of a tessellation figure.